【適性試験】SPI試験対策グラフの領域

SPI グラフの領域

SPIで出題されるグラフの問題を扱います。領域の問題が主になっています。

SPI グラフの問題のチュートリアル

注意：何も注意がない限り、以下、縦軸をY軸方向、横をX軸方向とします。要するに普通通りです。

中学校の範囲ですが、忘れている人も多くいるでしょう。すぐにx=2y+4のグラフを書けますか？義務教育と言えども、内容を覚えている保証はわかりません。

直線のグラフの形を覚えましょう。直線のグラフの形は、y=ax+bまたはx=ay+bで表現されます。たとえば、y=ax+bのグラフの形は以下のようになっています。

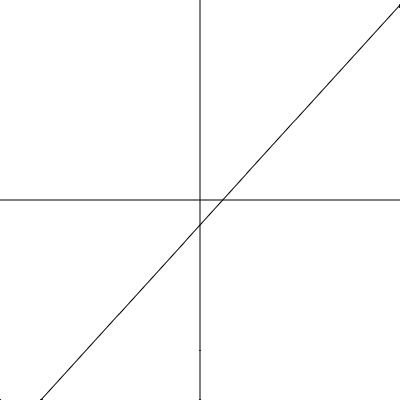
放物線は、y=ax²またはx=ay²の形で表現されています。
形は以下のようになっています。

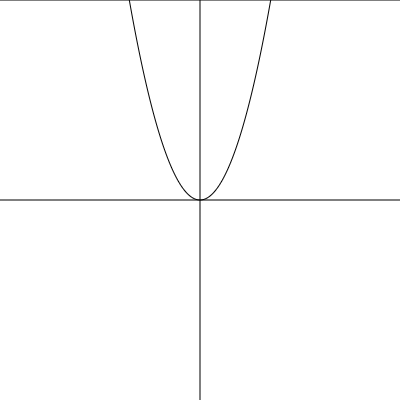
ちなみに↓にあるのは、x=ay²の場合です。↑がy=ax²です。

実際に、y-x+1>0の領域を図示してみましょう。

この式を変形させるとy>x-1です。これをみたす(x,y)全体を塗りつぶして図示すればいいわけですが…どちら側の領域でしょうか。

例えば、(x,y)=(0,0)は、y>x-1が成り立ちます。
例えば、(x,y)=(0,5)は、y>x-1が成り立ちます。
例えば、(x,y)=(0,-5)は、y>x-1が成り立ちません。

ここなどから、グラフのy軸方向、つまり上側を塗りつぶすべきであることがわかります。

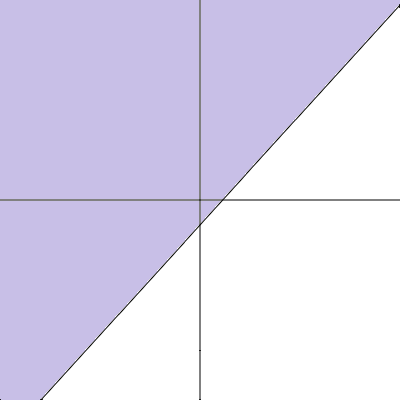
次に、x-3y²<0を図示してみましょう。
この不等式を変形すると、x<3y²という形になるので、x軸をもとに考えていきます。
x=3y²の概形は以下のようになります。3y²よりxが小さい部分を描画すればいいわけです。

↓が該当するグラフです。

このグラフが該当する領域は、先ほどと同様にやれば以下のようになります。

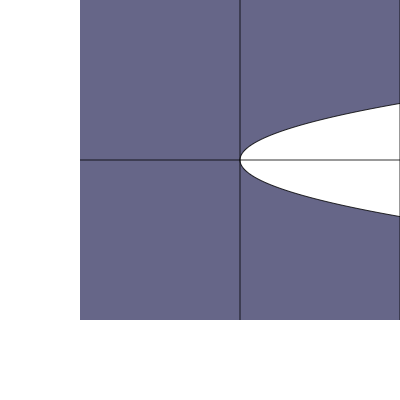
y>f(x)の場合は、グラフよりy軸方向（上側）に、x>f(y)の場合は、グラフよりx軸方向（右側）に。不等式の向きが逆なら逆方向に。不等式が示す領域を図示するときは、上のようにやれば簡単です。

グラフと不等式の問題は、必ず解けるようにしてください。

野菜と果物を、合計で20～50個仕入れます。
野菜は200円、果物は300円です。ただし、所持金は10000円のため、仕入れ数は限定されています。
野菜をX軸、果物をY軸にとって、提示された条件に整合する領域を図示してください。

解き方としては、条件をxとyの式で表現して、y=axまたはx=by+cのような形に整理することです。

野菜と果物の合計は20～50個だから、x+y≧20、x+y≦50が成り立ちます。
さらに、所持金は10000円のため、200x+300y≦10000を満たすことが条件です。
これらを図示すると、おおむね以下のようになります。ただし、境界は含みます。

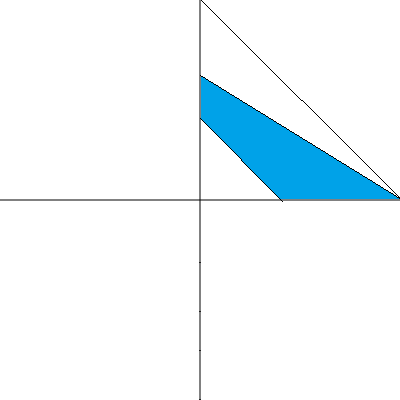
注意：図示の方法については、当ページ前半を参照してください。

文章題の条件を、グラフとして図示できるようにしましょう。実際に下のSPIグラフの領域の問題の自動生成ツールで練習してください。

2016.10.04　公開